Inada Conditions: An Overview

If you read economic papers especially those related to macroeconomics, you may have at some point read about Inada conditions. Maybe you are like, What the blazes are these conditions? What do they even mean?

Well, these conditions are in fact very important, not only in those fancy equations you see around and those mumbo jumbo, sorcery-like terms you read in papers but also for everyone like me and you.

Jargons aside! Let me help you to understand these conditions with ease!

An Overview

The Inada conditions are one of the crucial conditions in macroeconomics; they were named after Inada Ken-Ichi’s paper “On a Two-Sector Model of Economic Growth: Comments and a Generalization.”^[1]Inada, K. I. (1963). On a two-sector model of economic growth: Comments and a generalization. The Review of Economic Studies, 30(2), 119-127. These conditions have interestingly been fundamental in the theory of balanced growth.

Hirofumi Uzawa was primarily responsible for introducing these conditions in his paper “On a Two-Sector Model of Economic Growth.”^[2]Uzawa, H. (1961). On a two-sector model of economic growth. The Review of Economic Studies, 29(1), 40-47. Inada conditions are frequently applicable in production and utility functions.

Inada Conditions are the conditions that control the path of a function to guarantee a stable equilibrium. The conditions are mainly applied to production and utility functions because these functions involve a choice of inputs that maximize output.

Since there exist infinite possibilities for different input choices; among those possibilities, there is one and only one bundle of choice for inputs that maximizes output. It is in this regard that Inada Conditions provide conditions that ensure the existence of stable equilibrium.

Inada Conditions and Related Properties

The conditions are mainly two (2), however, they cannot independently ensure stable equilibrium as well as balanced growth path. There exist additional properties that can accompany these conditions. The three main properties are:

Non-negativity: the function shall be strictly positive for any combinations of labor and capital allocated to the production function.
Diminishing marginal productivity: this property sets out conditions that each unit of input of production added will relatively result in reduced productivity. Specifically, this property prevents that the production function can increase infinitely, causing the second condition to not hold.
Asymptotic conditions:As capital approaches zero, the marginal product of capital also approaches infinity, and as capital approaches infinity, the marginal product of capital also approaches zero. This demonstrates that marginal productivity is inversely related to capital accumulation. This can also apply to labor.

Even though the first two properties are not directly related to inada conditions, they clearly set out a crucial restriction to the solution of output. Let us now take a look at each property to understand why these conditions need to hold to ensure a stable equilibrium and balanced growth path.

Non-negativity

The non-negativity limits the function to be irrelevant and meaningless because, for sure, there is no firm that can produce negative output; hence, the output produced has to be strictly positive or at least equal to zero. In other words, “there has to be nothing or something!”

The above expression can be written mathematically as:

$f(k) \geq 0 \; \; \forall \; \; k \in \mathbb{R}^n_+$

We can say that, for all non-negative choices of inputs (say, capital), the output (say, production) function would give us non-negative output, but we can flexibly allow the output to be equal to zero.

Diminishing Marginal Productivity

This property controls the motion/dynamics of productivity against capital and/or labor inputs, or simply any other inputs to the function because the changes in productivity based on inputs will change over time before reaching the steady state.

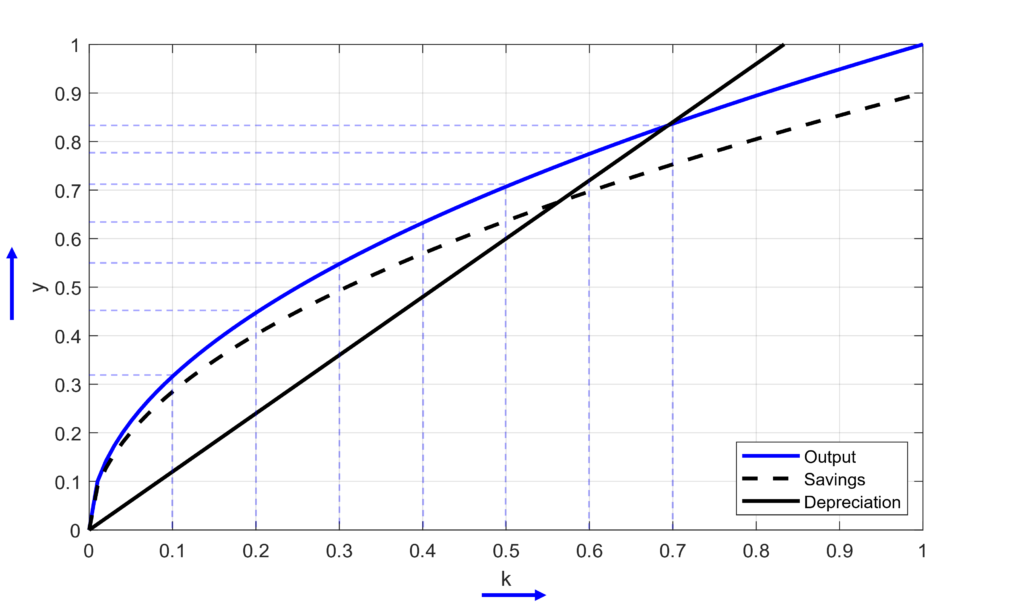
Solow-Swan Model showing Inada conditions. — **Figure 1:**Solow Growth Model show clearly Inada conditions

Simply put, as more input is added for production, the production grows faster, but when the production function approaches steady state, the marginal productivity of that input reduces (i.e, less efficient).

In figure 1, you can see that as the distance between dashed lines on the y-axis (output) shrinks as the x-axis (capital) values approach one. It implies that all inputs in production are not equally efficient. At the beginning of production, a unit increase in inputs (i.e., labor or capital) will be extremely important, but as you add more inputs, their efficiency will decrease over and over again until an additional input will no longer add anything.

The expressions can also be written mathematically as:

$\frac{\partial f}{\partial k} > 0$ , and $\frac{\partial^2f}{\partial k^2} < 0$

Asymptotic Conditions

This condition is technically what leads us to the Inada conditions themselves. The asymptotic conditions can be understood in this way; as input approaches zero, the marginal product of that input approaches infinite, or if input approaches infinity, the marginal product of that input approaches zero.

The inada conditions are defined using Hôpital’s rule as follows:

$\lim_{k\to 0}f'(k) = \infty$

$\lim_{k\to\infty}f'(k) = 0$

Where: $f'(k) = \frac{\partial f}{\partial k}$ ; $k = \frac{K}{AL}$ ^[3]The AL is the effective (A) labor (L).

So, the above conditions are all you need for a certain function to ensure a stable equilibrium of a balanced growth path.

The conditions imply that (1) at the beginning of the growth path, a small change in capital accumulation induces large changes in output, but (2) as the capital continues to increase towards infinity, the responsiveness in productivity reduces towards zero.

Other Posts:

The price you pay on food is high: What do you do?

Inflation Volatility in Rwanda

Analogy for Inada Conditions

Let me use the example of a person called Kalinda who has gone a day and half without food to explain the Inada conditions in layman’s terms.

In that case, if someone gives Kalinda a piece of cake, he will be extremely happy and excited.

If Kalinda keeps eating more pieces of cake, say every two hours, his levels of happiness for an additional cake will reduce slowly to an extent where it will be close to zero.

Taking cake as a sort of input and happiness and excitement as output; hence, we can write this example as inada conditions:

$\lim_{c\to 0}U'(c) = \infty$ : A small piece of cake made Kalinda extremely happy and was very important to his life because it saved him from starving to death.

$\lim_{c\to\infty}U'(c) = 0$ : Many more pieces of cake did not make Kalinda as happy as the ones he ate when he was starving due to their little importance to his life.

Bottom Line

Inada conditions are crucial macroeconomic conditions that will enable a function to have balanced growth with a stable equilibrium.

Inada conditions have other related properties. These properties have complementary conditions, like the non-negativity condition, which prevents absurd output values, diminishing marginal productivity, which demonstrates inefficiencies in inputs over time.

As noted earlier, inada conditions are crucial, especially when determining equilibrium and growth path of function explained by certain inputs. If these conditions are satisfied, then a function’s stability in equilibrium is guaranteed.

References[+]

References
↑1	Inada, K. I. (1963). On a two-sector model of economic growth: Comments and a generalization. The Review of Economic Studies, 30(2), 119-127.
↑2	Uzawa, H. (1961). On a two-sector model of economic growth. The Review of Economic Studies, 29(1), 40-47.
↑3	The AL is the effective (A) labor (L).

Kazana Leonidas